update: 25/01/26
Method
Geometric references: Lamé curves, Voronoi diagrams and René Descartes.
Note on the method
The method described here originates from a long-term practice, developed and consolidated over more than twelve years. It is a form of research built through making, based on the repeated application of a simple rule rather than on the theoretical definition of a closed system.
The Absorbed Structure
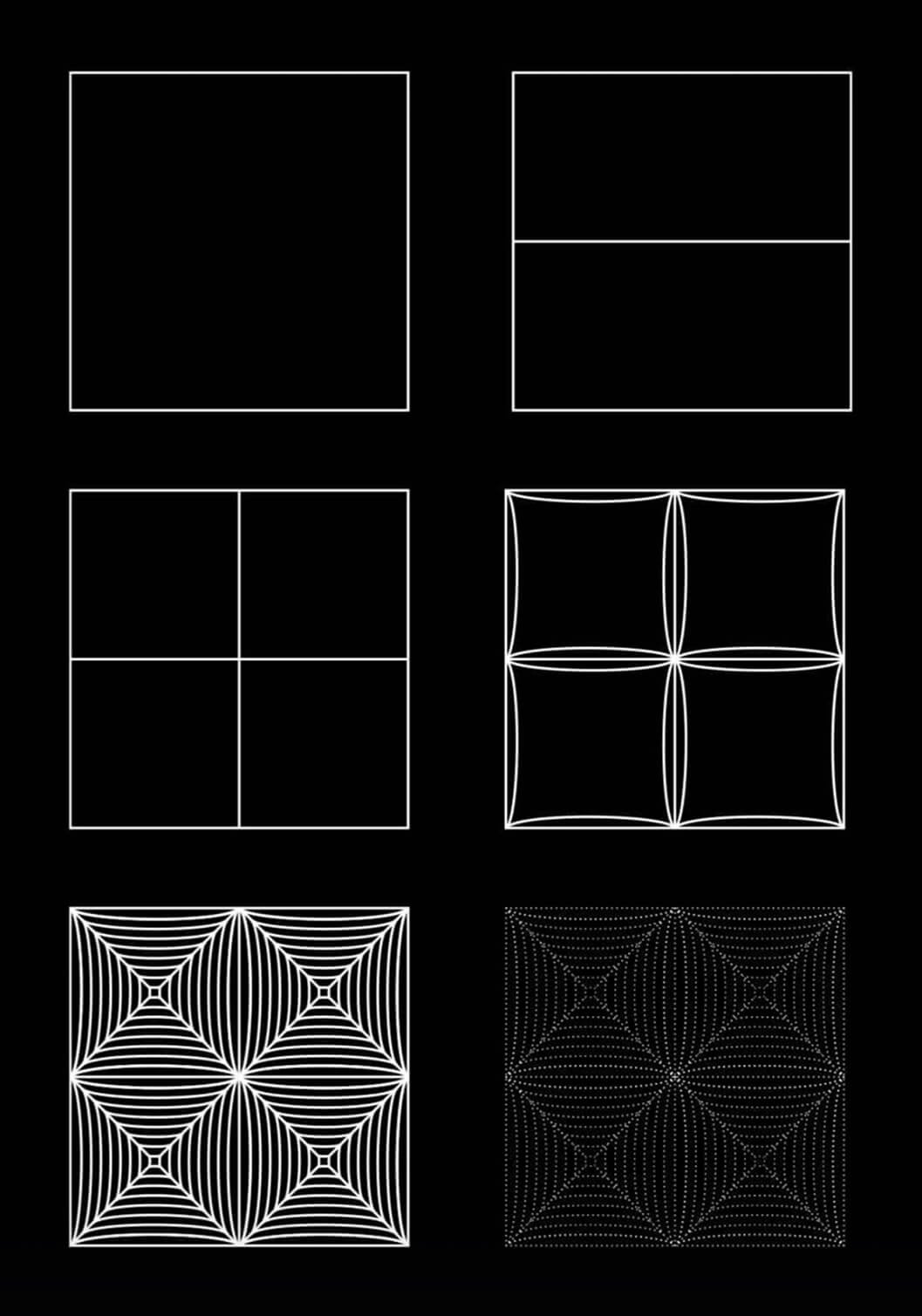
The work always begins from an essential base: a geometric grid, a matrix. At the points of intersection, I establish the poles from which the curved lines originate. The lines are constructed manually, one at a time, maintaining a constant distance while the curvature progressively increases.
As the work advances, the initial grid gradually loses legibility. It is not erased, but absorbed through the accumulation of marks. It continues to orient the movement of the curves, while ceasing to function as a rigid framework. What remains visible is a continuous field — a new organization of space built over time.
Process and Variability
I do not work toward a predefined image. The final outcome is not decided in advance; it is the direct consequence of the process.
The rule remains unchanged, but each work varies according to two elements: the initial arrangement of the poles (the matrix), and the way the lines are drawn (continuous, interrupted, dotted). These choices are not decorative. They are structural, determining whether the field appears dense and compact or more open and vibrating.
Lamé Curves (Superellipses)
Over time, a geometric coherence emerged that went beyond freehand drawing. Further investigation revealed a structural correspondence with Lamé curves (superellipses). It is important to clarify that the method does not originate from mathematical formulas; this reference emerged a posteriori.
The manual practice appears to physically explore the same territory that theories such as Gielis’ Superformula describe in formal terms: different paths converging toward the principles that govern the formation of shapes in nature, from the square to the circle through intermediate stages.
The text From Pythagoras to Fourier and From Geometry to Nature provides a theoretical context within which the reference to Lamé becomes legible.
“From Pythagoras to Fourier and From Geometry to Nature” provides a theoretical context in which the reference to Lamé becomes readable.
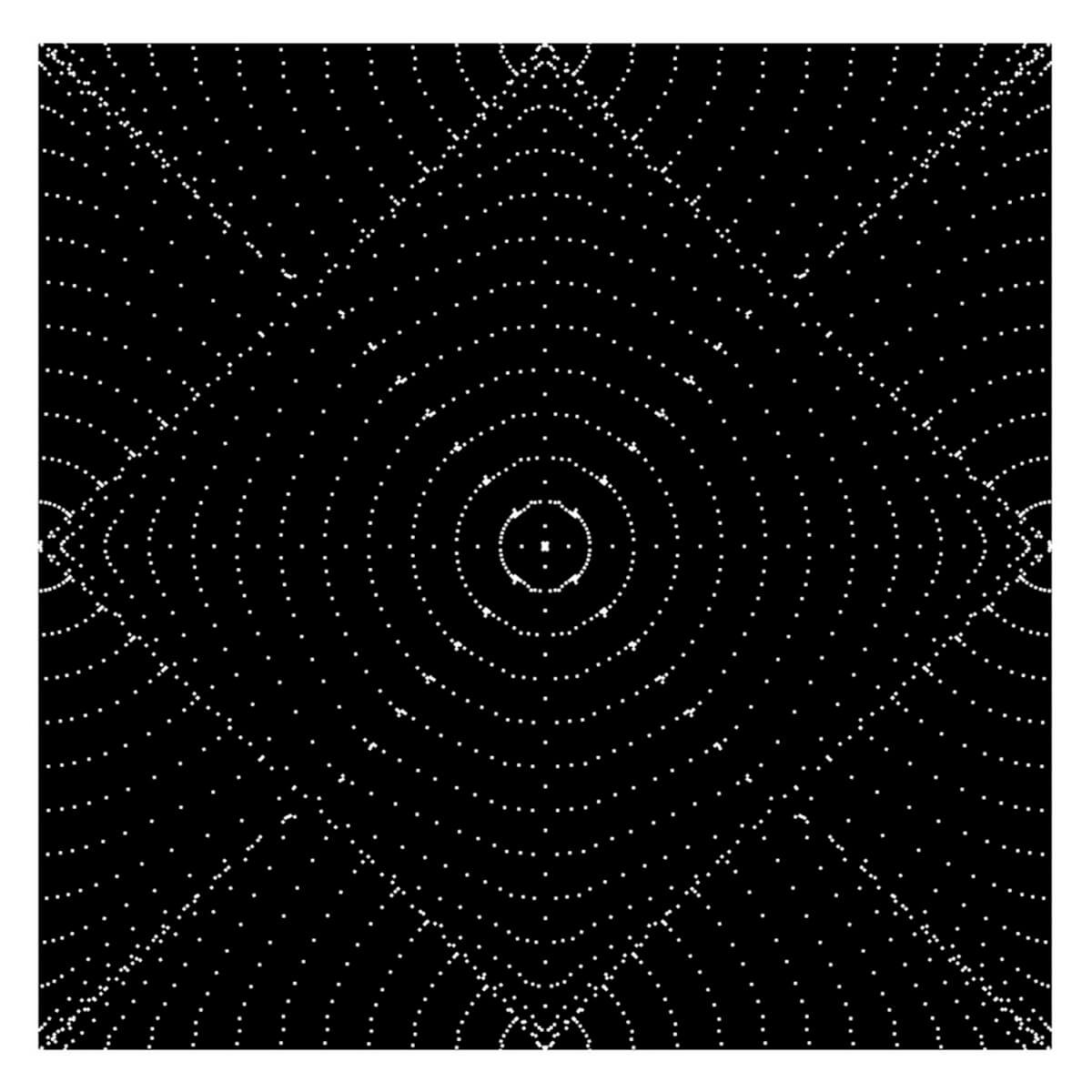
Voronoi Diagrams
A Voronoi diagram is a geometric tool that divides space into regions of proximity starting from a set of seeds. This division defines clear boundaries and areas of belonging, but it does not describe how the interior of each region is organized, nor how the seed relates to the boundary zones of its cell.
Over time, several theoretical models have addressed this limitation by introducing internal readings of Voronoi cells, such as the medial axis, the straight skeleton, or distance fields from the boundary. These tools distinguish peripheral and internal zones and identify central structures, but they do so through instantaneous or convergent outcomes in which the generating process remains invisible.
When placed in relation to a Voronoi structure, the method described here occupies a different position. It does not aim to correct or optimize the subdivision, but to traverse it. The propagation of lines, initially constrained by the cell boundaries, generates transition zones and areas of greater saturation that do not necessarily coincide with the seed or with a geometric center. In this way, the method makes visible the behavior of space as it forms, rather than its final organization.
As in skeletal models, the process inevitably leads to the formation of an internal region. However, while in the straight skeleton this region always resolves into a defined central structure, in this method centrality manifests as a condition of saturation. It may concentrate, diffuse, or fragment depending on the initial configuration and the evolution of the process. The center is therefore not an objective or a point to be reached, but the outcome of a behavior unfolding over time.
Working with Voronoi structures, the method also suggests recurring readings. The periphery does not act as a marginal zone, but as an active area of transition, where propagation encounters resistance and deviation capable of influencing the entire field. The initial seed tends to lose its role as a central reference, becoming internal or peripheral with respect to the emerging structures, introducing a distinction between geometric origin and spatial relevance.
Unlike skeletal models, the method is not conceived to converge toward a single optimized solution. Internal structures emerge through interference and accumulation, making visible unstable or transitional configurations that other approaches tend to normalize. Symmetries and asymmetries are not neutralized, but amplified, suggesting a gradual continuity between boundary and interior rather than a sharp separation.
In this sense, the method does not seek to replace existing readings of the Voronoi diagram, but adds a possible interpretative key that can coexist with them, introducing a process-based and temporal dimension that highlights specific characteristics.
Descartes and the logic of vortices
(historical and conceptual reference)
In his theory of vortices, René Descartes describes space as a continuous plenum, devoid of voids, organized into regions of influence around centers. Each vortex occupies a portion of space determined by its equilibrium with adjacent vortices: boundaries are not predefined, but emerge as zones of contact between competing fields.
Although these representations do not possess the mathematical rigor of modern Voronoi diagrams, they share a fundamental principle: space is assigned to a center up to the point where the influence of another center becomes equivalent. In this sense, the theory of vortices can be read as an intuitive and qualitative formulation of a space partition based on centers and relations of balance.
The method described here operates on a different plane, yet enters into dialogue with this logic. Unlike the Voronoi diagram, which defines boundaries between regions, the method does not limit itself to subdividing space, but observes its internal formation. Once a territory—explicit or implicit—is established, the propagation of lines makes visible how that space is filled, how peripheral zones are structured, and how a central region emerges through accumulation and interference.
The relationship with Descartes is therefore neither formal nor historical, but structural. The theory of vortices introduces the idea of a full space organized through fields of influence; the method assumes its operational consequence, translating it into a controlled visual process. The center is not an imposed point, but an emergent condition. The boundary is not an abstract limit, but the result of encounters between propagations.
The method neither extends nor corrects Cartesian theory, nor does it propose a physical reading of space. It does, however, share a fundamental premise: space is not a neutral container, but something that takes shape through relations, contact, and accumulation. Within this framework, the method can be understood as a contemporary and operative reading of that same intuition, applied not to cosmology, but to the visual construction of the field.
Considerations on the Method
1 – Relations over Object > Given a matrix, the accumulation of lines dissolves the individual starting elements (the cells). What becomes legible is no longer the initial scheme, but the relations and tensions created between the poles.
2 – Construction by Accumulation > Space is not given, but constructed. From an empty plane, a complex surface develops through the repetitive and patient application of an elementary rule. The field defines itself through continuity and layering.
3 – Formation of Space > The method does not describe a space, but observes how space is formed. It is not a static representation, but the visible trace of a geometric behavior that evolves as it is executed.
4 – Integration of the Variable > The process accepts the manual nature of the execution. Slight deviations in curvature or distance are not corrected as errors but absorbed by the structure. The system is robust enough to integrate these irregularities, transforming a rigid geometry into a more fluid configuration.
5 – Emergent Dynamics > Despite starting from fixed and regular coordinates, the outcome is a dynamic configuration. The initial Cartesian coordinates fade into the background, replaced by new directions suggested by the flow of the lines. Each drawn line is potentially a new boundary from which the matrix can expand further.
Examples










Metodo
Nota sul metodo
Il metodo qui descritto nasce da una pratica di lungo corso, sviluppata e consolidata nel tempo nell’arco di oltre dodici anni. È una ricerca costruita nel fare, attraverso l’applicazione ripetuta di una regola semplice, più che attraverso la definizione teorica di un sistema chiuso.
La Struttura Assorbita
Il lavoro inizia sempre da una base essenziale: una griglia geometrica, una matrice. Nei punti di intersezione fisso i poli di origine delle linee curve. Le linee vengono costruite manualmente, una alla volta, mantenendo una distanza costante mentre la curvatura aumenta progressivamente.
Con l’avanzare del lavoro, la griglia iniziale perde leggibilità. Non viene cancellata, ma assorbita dall’accumulo dei segni. Continua a orientare l’andamento delle curve, ma smette di funzionare come gabbia rigida. Quello che resta visibile è un campo continuo, una nuova organizzazione dello spazio costruita nel tempo.
Processo e Variabilità
Non lavoro per realizzare un’immagine già definita. Il risultato finale non è deciso a priori: è la conseguenza diretta del processo.
La regola rimane invariata, ma ogni lavoro cambia in base a due elementi: la disposizione iniziale dei poli (la matrice) e il modo in cui le linee vengono tracciate (continue, interrotte, puntinate). Queste scelte non sono decorative. Sono strutturali: determinano se il campo apparirà più denso e compatto o più rarefatto e vibrante.
Curva di Lamé (Superellisse)
Nel tempo è emersa una coerenza geometrica che andava oltre il disegno a mano libera. Approfondendo la ricerca, ho riscontrato una corrispondenza strutturale con le Curve di Lamé (superellissi). È importante chiarire che il metodo non nasce da formule matematiche: il riferimento è una scoperta a posteriori.
La pratica manuale sembra esplorare fisicamente lo stesso territorio che teorie come la Superformula di Gielis descrivono in modo formale: un avvicinamento, per vie diverse, alle logiche che regolano la formazione delle forme in natura, dal quadrato al cerchio, attraversando stadi intermedi.
“From Pythagoras to Fourier and From Geometry to Nature” offre un contesto teorico all’interno del quale il riferimento a Lamé diventa leggibile.
Diagrammi di Voronoi
Il diagramma di Voronoi è uno strumento geometrico che suddivide lo spazio in regioni di prossimità a partire da un insieme di semi. Questa suddivisione definisce confini netti e aree di appartenenza, ma non fornisce indicazioni su come lo spazio interno a ciascuna regione si organizzi, né su come il seme si relazioni alle zone di confine della propria cella.
Nel tempo, diversi modelli teorici hanno affrontato questa mancanza introducendo letture interne alle celle di Voronoi, come lo scheletro mediale, lo straight skeleton o i campi di distanza dal bordo. Questi strumenti permettono di distinguere zone periferiche e zone interne, individuando strutture centrali, ma lo fanno attraverso esiti istantanei o convergenti, in cui il processo che le genera resta invisibile.
Quando viene messo in relazione con una struttura di Voronoi, il metodo qui descritto si colloca in una posizione diversa. Non interviene per correggere o ottimizzare la suddivisione, ma per attraversarla. La propagazione delle linee, inizialmente vincolata ai bordi delle celle, genera zone di transizione e aree di maggiore saturazione che non coincidono necessariamente con il seme né con un centro geometrico. In questo modo, il metodo rende leggibile il comportamento dello spazio mentre si forma, più che la sua organizzazione finale.
Come nei modelli scheletrici, il processo conduce inevitabilmente alla formazione di una regione interna. Tuttavia, mentre nello straight skeleton questa regione si risolve sempre in una struttura centrale definita, nel metodo la centralità si manifesta come una condizione di saturazione. Può concentrarsi, diffondersi o frammentarsi in base alla configurazione iniziale e all’evoluzione del processo. Il centro non è quindi un obiettivo né un punto da raggiungere, ma l’esito di un comportamento che si sviluppa nel tempo.
Nel lavorare su strutture di Voronoi, il metodo sembra inoltre suggerire alcune letture ricorrenti. La periferia non appare come una semplice zona marginale, ma come un’area attiva di transizione, in cui la propagazione incontra resistenze e deviazioni capaci di influenzare l’intero campo. Il seme iniziale tende a perdere il ruolo di riferimento centrale, potendo risultare interno o periferico rispetto alle strutture emerse, introducendo una distinzione tra origine geometrica e rilevanza spaziale.
A differenza dei modelli scheletrici, il metodo non è concepito per convergere verso una soluzione unica o ottimizzata. Le strutture interne emergono per interferenza e accumulo, rendendo visibili configurazioni instabili o transitorie che altri approcci tendono a normalizzare. Simmetrie e asimmetrie non vengono neutralizzate, ma amplificate, suggerendo una continuità graduale tra confine e interno piuttosto che una separazione netta.
In questo senso, il metodo non intende sostituire le letture esistenti del diagramma di Voronoi, ma aggiunge una possibile chiave di interpretazione sovrapponibile a esse, introducendo una dimensione processuale e temporale che ne mette in evidenza alcune peculiarità.
Cartesio e la logica dei vortici
(riferimento storico e concettuale)
Nella teoria dei vortici, René Descartes descrive lo spazio come un continuum pieno, privo di vuoti, organizzato in regioni di influenza attorno a centri. Ogni vortice occupa una porzione di spazio determinata dall’equilibrio con i vortici adiacenti: i confini non sono stabiliti a priori, ma emergono come zone di contatto tra campi concorrenti.
Sebbene queste rappresentazioni non abbiano lo statuto matematico dei moderni diagrammi di Voronoi, condividono con essi un principio fondamentale: lo spazio viene assegnato a un centro fino al punto in cui l’influenza di un altro centro diventa equivalente. In questo senso, la teoria dei vortici può essere letta come una formulazione intuitiva e qualitativa di una partizione dello spazio basata su centri e relazioni di equilibrio.
Il metodo qui descritto si colloca su un piano diverso, ma dialoga con questa logica. A differenza del diagramma di Voronoi, che definisce i confini tra regioni, il metodo non si limita a suddividere lo spazio, ma ne osserva la formazione interna. Una volta stabilito un territorio — esplicito o implicito — il processo di propagazione delle linee rende visibile come quello spazio si riempie, come si strutturano le zone periferiche e come una regione centrale emerga per accumulo e interferenza.
Il rapporto con Cartesio non è formale né storico, ma strutturale. La teoria dei vortici introduce l’idea di uno spazio pieno, organizzato per campi di influenza; il metodo ne assume la conseguenza operativa, traducendola in un processo visivo controllato. Il centro non è un punto imposto, ma una condizione che emerge. Il confine non è un limite astratto, ma il risultato dell’incontro tra propagazioni.
Il metodo non estende né corregge la teoria cartesiana, né intende proporre una lettura fisica dello spazio. Ne condivide però un presupposto essenziale: lo spazio non è un contenitore neutro, ma qualcosa che prende forma attraverso relazioni, contatti e accumuli. In questo quadro, il metodo può essere inteso come una possibile lettura contemporanea e operativa di quella stessa intuizione, applicata non alla cosmologia, ma alla costruzione visiva del campo.
Considerazioni
1 – Relazioni su Oggetto > Data una matrice, l’accumulo delle linee dissolve i singoli elementi di partenza (le celle). Ciò che diventa leggibile non è più lo schema iniziale, ma le relazioni e le tensioni che si instaurano tra i poli.
2 – Costruzione per Accumulo > Lo spazio non è dato, ma costruito. Da un piano vuoto si sviluppa una superficie complessa attraverso l’applicazione ripetitiva e paziente di una regola elementare. Il campo si definisce per continuità e sovrapposizione.
3 – Formazione dello Spazio > Il metodo non descrive uno spazio, ma osserva come lo spazio si forma. Non è una rappresentazione statica, ma la traccia visibile di un comportamento geometrico che evolve mentre viene eseguito.
4 – Integrazione della Variabile > Il processo accetta la natura manuale dell’esecuzione. Le lievi deviazioni nella curvatura o nella distanza non vengono corrette come errori, ma assorbite dalla struttura. Il sistema è sufficientemente robusto da integrare queste irregolarità, trasformando una geometria rigida in una configurazione più fluida.
5 – Dinamica Emergente > Pur partendo da coordinate fisse e regolari, l’esito è una configurazione dinamica. Le coordinate cartesiane iniziali passano in secondo piano, sostituite da nuove direzioni suggerite dal fluire delle linee.
Ogni intersezione generata dal processo è potenzialmente un nuovo punto di origine da cui la matrice può espandersi ulteriormente.
Esempi












